Tenemos que producir la máxima cantidad de dos productos en cierta proporcion. Puede ser bebida y comida para una poblacion, o las ruedas y el cuadro de una bicicleta. El caso es que esos dos productos acaban teniendo un precio «interno» que no se parece en nada a lo que cuentan de la oferta y demanda.
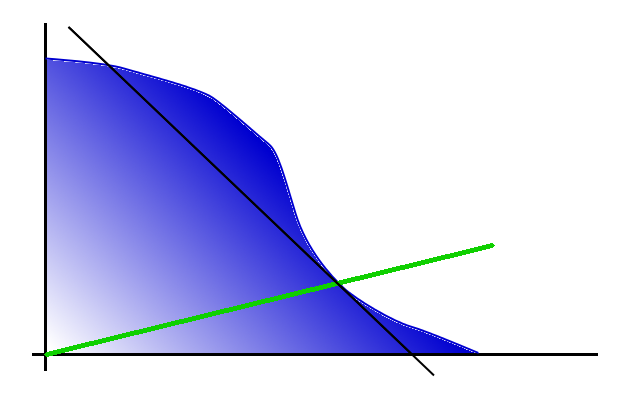
Pintamos un grafico poniendo en horizontal la cantidad producida de uno de los elementos (digamos, ruedas) y en vertical la del otro (digamos, cuadros). Como la gente se puede poner a hacer bien uno, bien otro, tendremos la superficie azul de posibilidades, cuyo limite lo forma una curva de pendiente variable, aunque siempre en la misma dirección si no hay algun efecto colateral: cuando un grupo de gente deja de fabricar uno de los productos, la cantidad del otro no baja, y seguramente subira porque algunos se podran a fabricar el otro.
La linea que indica la proporcion que queremos la he pintado en verde. Nuestro punto optimo es pues cuando la linea verde se cruza con el final de la superficie azul.
Y en los alrededores de esa curva, la linea verde no tiene ningun papel más alla de seleccionar el punto de corte. Si hay alguna acción, comercial o social, que pueda definir ese punto, vendra dada por la derivada de la curva, la tangente que he pintado en negro.
Pero… a lo que he entendido, resulta que esa tangente solo funciona cuando esta encima de la curva. O mas concretamente, cuando la curva se forma a partir de una union de una cantidad grande de cuadrillas, trabajadores o empresas, cada uno en capacidad de aportar un pequeño grano al total. En ese caso la curva total se construye on el truco de Kantorovich, ordenando a cada cuadrilla segun su capacidad de producir una cosa respecto de la otra. Cuando estemos produciendo cero ruedas, todos estaran haciendo cuadros y la curva estara en su punto maximo en el eje vertical. Retiramos de cuadros (y ponemos a hacer ruedas) a la cuadrilla mas torpe haciendo cuadros y la curva se ira dibujando de forma muy plana, cada vez inclinandose mas segun vamos retirando a grupos que eran mejores haciendo cuadros. Asi que esa curva siempre tiene la tangente por encima, y el punto donde se corte con la linea verde es el punto donde debemos separar las cuadrillas entre una y otra tarea: la pendiente de ese punto marca el precio oculto, el precio al cual cada cuadrilla fabricara lo que es mas eficaz.
Ahora, ¿que pasa si por la construccion (pocas cuadrillas, monopolios, etc) la curva es tal que la tangente queda por debajo de ella? Pues no tengo ni idea, pero a primera vista no parece que este precio oculto intrinseco sirva de nada. En este caso es mas eficaz olvidarse de la linea verde y producir unos dias mas de una cosa y otros mas de otra, de forma que al final la combinacion del stock produzca el objetivo. Vamos, a base de añadir variabilidad en el tiempo sustituimos la superficie de produccion por su envolvente convexa. Quizas la tangente en este caso da alguna pista sobre esa envolvente, o simplemente una cota.
Otra idea curiosa es que este precio, aunque es algo que se paga a cada cuadrilla, solo es un «dinero interno» que existe dentro de esta produccion concreta. El resultado visto desde fuera es que se han gastado unas horas de trabajo y se han producido tantas bicicletas. Para otra produccion distinta el «precio» corresponderia a otra «moneda» diferente.
Deja una respuesta