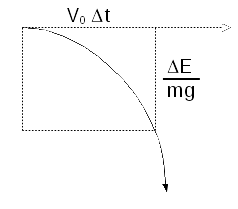
Abundando en el post sobre Newton, quizas la forma más corta de empezar a ver la mecanica cuantica es el movimiento en un campo de fuerzas constante, como el de un condensador, o como el de la caida parabolica de Galileo de toda la vida:
El area del rectangulo mide
\(v_0 \Delta t \Delta E \over m g\)
Y por tanto, lo que nos dice el principio de indeterminacion (todavia el de Sommerfeld, en este caso: \(\Delta t \Delta E \ge \hbar\)) es que no podemos construir un rectangulo de area infinitesimalmente pequeña. El area minima, si estamos haciendo «gravedad galileana cuantica», seria \(v_0 \hbar \over m g\). O en general, con una fuerza constante de intensidad F, \(v_0 \hbar \over F\)
Deja una respuesta